import numpy as np
def remove_i(x, i):
"""Drops the ith element of an array."""
shape = (x.shape[0]-1,) + x.shape[1:]
y = np.empty(shape, dtype=float)
y[:i] = x[:i]
y[i:] = x[i+1:]
return y
def a(i, x, G, m):
"""The acceleration of the ith mass."""
x_i = x[i]
x_j = remove_i(x, i) # don't compute on itself
m_j = remove_i(m, i)
diff = x_j - x_i
mag3 = np.sum(diff**2, axis=1)**1.5
# compute acceleration on ith mass
result = G * np.sum(diff * (m_j / mag3)[:,np.newaxis], axis=0)
return resultIntroduction to parallel computing
Oregon State University
2025-02-24
Introduction to parallel computing (in Python)
If you want more, check out CS 475/575 Parallel Programming.
Approaching parallelism
- How do I do many things at once?
- How do I do one thing faster?
Computer: perform many simultaneous tasks
Developer: determine dependencies between code and data
Up until now: serial thinking, like “x then y then z”
Benefit of parallelism: problems execute faster—sometimes much faster.
Downside to parallelism: harder to program, debug, open files, print to screen.
Why go parallel?
Important
First: wait until your code works and you need it.
- The problem creates or requires too much data for a normal machine.
- The sun would explode before the computation would finish.
- The algorithm is easy to parallelize.
- The physics itself cannot be simulated at all with smaller resources.
Scale and scalability

“Scale and Scalability” book cover
Scale and scalability
Scale: size of problem
Scale is proportional to number of processes \(P\) used, and thus the maximum degree of parallelism possible.
FLOPS: number of floating-point operations per second
Scaling up code
Scale up slowly—start with one processor, then 10, 100, etc.
scalability: how easy or hard it is to scale code
Strong scaling
strong scaling: how runtime changes as a function of processor number for a fixed total problem size.
speedup \(s\) ratio of time on one processor (\(t_1\)) to time on \(P\) processors (\(t_P\)):
\[ s(P) = \frac{t_1}{t_P} \]
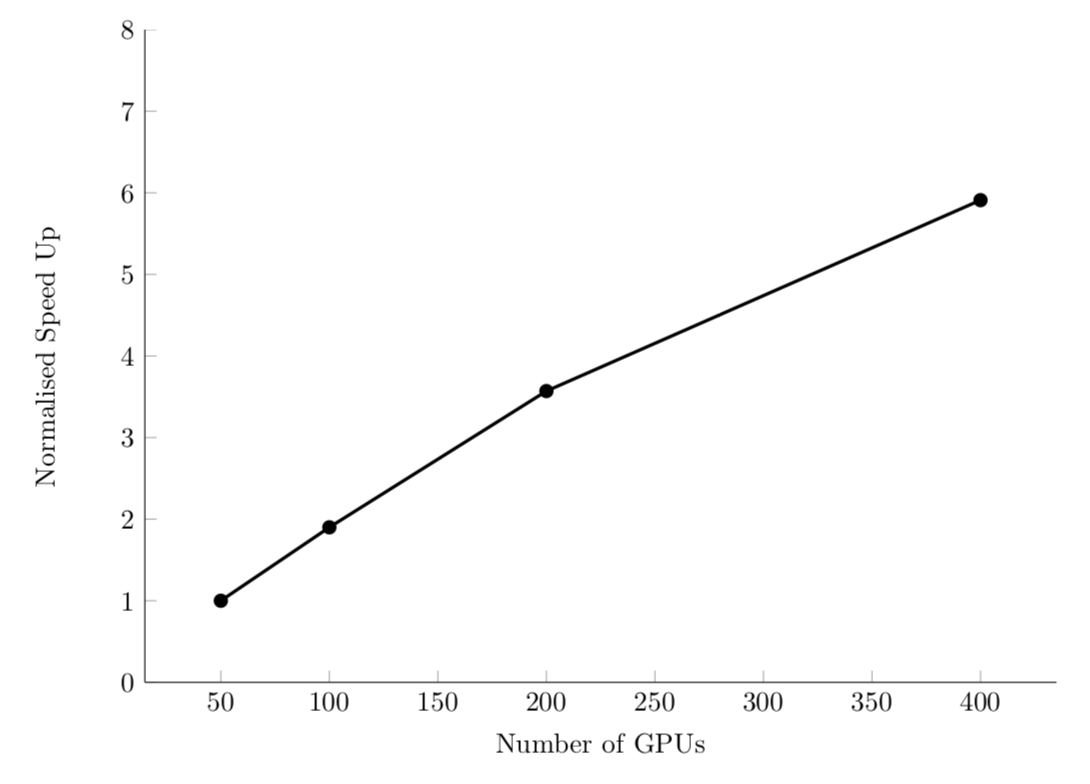
Strong scaling
Efficient system: linear strong scaling speedup.
For example, PyFR computational fluid dynamics code:
Weak scaling
weak scaling: how runtime changes as a function of processor number for a fixed problem size per processor
sizeup \(z\) for a problem size \(N\):
\[ z(P) = \frac{t_1}{t_P} \times \frac{N_P}{N_1} \]
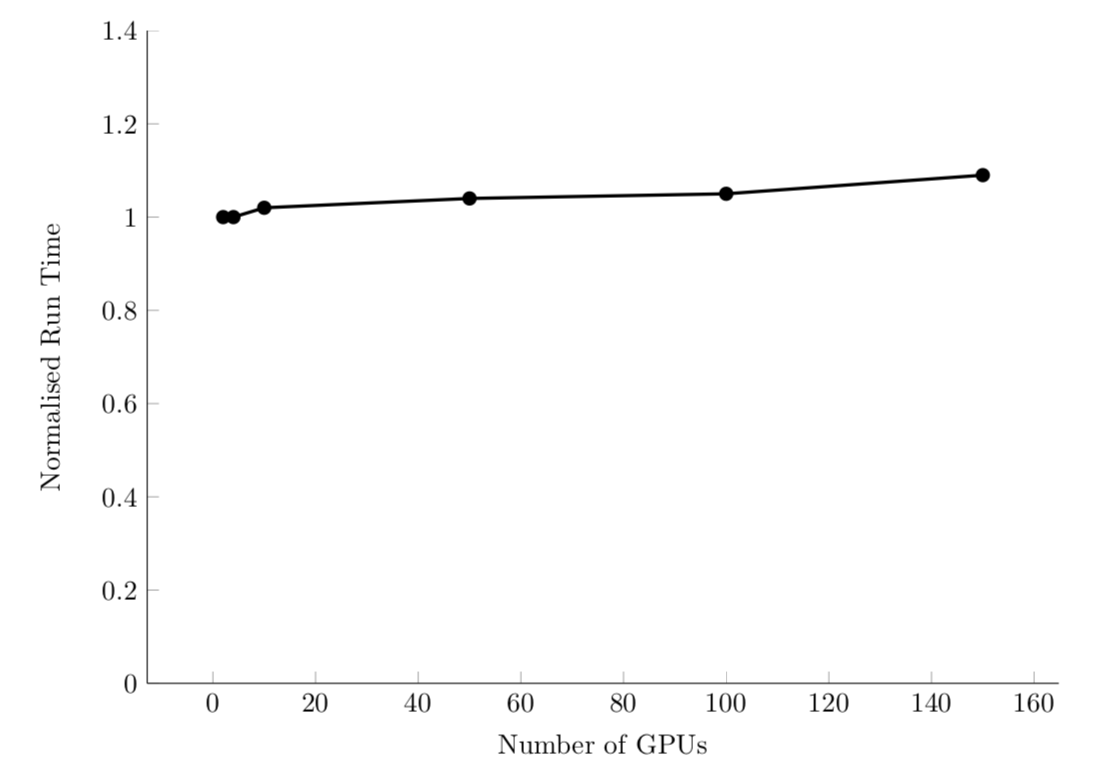
Weak scaling
Efficient system: linear sizeup. Or, constant time with additional processors/problem size.
For example, PyFR computational fluid dynamics code:
Amdahl’s Law
Some fraction of an algorithm, \(α\), cannot be parallelized.
Then, the maximum speedup/sizeup for \(P\) processors is:
\[ \max( s(P) ) = \frac{1}{\alpha - \frac{1-\alpha}{P}} \]
The theoretically max speedup is:
\[ \max(s) = \frac{1}{\alpha} \]
Types of problems
embarassingly parallel: algorithms with a high degree of independence and little communication between parts
Examples: summing large arrays, matrix multiplication, Monte Carlo simulations, some optimization approaches (e.g., stochastic and genetic algorithms)
Other algorithms have unavoidable bottlenecks: inverting a matrix, ODE integration, etc.
Not all hope is lost! Some parts may still benefit from parallelization.
Example: N-body problem
Generalization of the classic two-body problem that governs the equations of motion for two masses. From Newton’s law of gravity:
\[ \frac{dp}{dt} = G \frac{m_1 m_2}{r^2} \]
Equations of motion
\[ \begin{align} \mathbf{x}_{i,s} &= G \sum_{j=1, i \neq j} \frac{m_j (\mathbf{x}_{j,s-1} - \mathbf{x}_{i,s-1})}{||\mathbf{x}_{j,s-1} - \mathbf{x}_{i,s-1}||^3} \Delta t^2 + \mathbf{v}_{i,s-1} \Delta t + \mathbf{x}_{i,s-1} \\ \mathbf{v}_{i,s} &= G \sum_{j=1, i \neq j} \frac{m_j (\mathbf{x}_{j,s-1} - \mathbf{x}_{i,s-1})}{||\mathbf{x}_{j,s-1} - \mathbf{x}_{i,s-1}||^3} \Delta t + \mathbf{v}_{i,s-1} \end{align} \]
No parallelism
def timestep(x0, v0, G, m, dt):
"""Computes the next position and velocity for all masses given
initial conditions and a time step size.
"""
N = len(x0)
x1 = np.empty(x0.shape, dtype=float)
v1 = np.empty(v0.shape, dtype=float)
for i in range(N): # update locations for all masses each step
a_i0 = a(i, x0, G, m)
v1[i] = a_i0 * dt + v0[i]
x1[i] = a_i0 * dt**2 + v0[i] * dt + x0[i]
return x1, v1
def initial_cond(N, D):
"""Generates initial conditions for N unity masses at rest
starting at random positions in D-dimensional space.
"""
x0 = np.random.rand(N, D) # use random initial locations
v0 = np.zeros((N, D), dtype=float)
m = np.ones(N, dtype=float)
return x0, v0, mGenerating initial conditions and taking one timestep:
Driver function that simulates \(S\) time steps:
Measuring performance
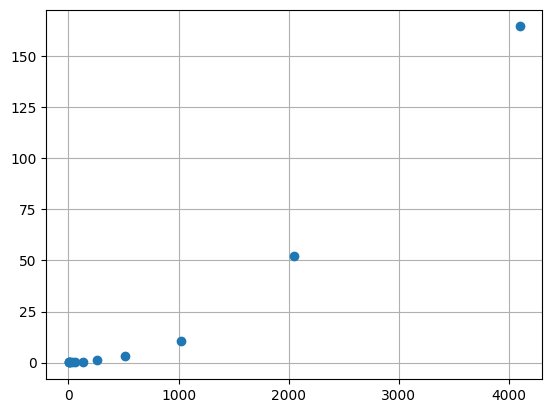
Does the problem scale quadratically?
Threads
- Threads perform work and are not blocked by work of other threads.
- Threads can communicate with each other through state
Threads: probably don’t use in Python.
- All threads execute in the same process as Python itself.
- Where to use? If you have high latency tasks where you can use spare time for another task (e.g., downloading a large file)
N-body with threading
from threading import Thread
class Worker(Thread):
"""Computes x, v, and a of the ith body."""
def __init__(self, *args, **kwargs):
super(Worker, self).__init__(*args, **kwargs)
self.inputs = [] # buffer of work for thraeds
self.results = [] # buffer of return values
self.running = True # setting to False causes run() to end safely
self.daemon = True # allow thread to be terminated with Python
self.start()
def run(self):
while self.running:
if len(self.inputs) == 0: # check for work
continue
i, x0, v0, G, m, dt = self.inputs.pop(0)
a_i0 = a(i, x0, G, m) # body of original timestep()
v_i1 = a_i0 * dt + v0[i]
x_i1 = a_i0 * dt**2 + v0[i] * dt + x0[i]
result = (i, x_i1, v_i1)
self.results.append(result)Thread pools
Expensive to create and start threads, so create pool that persists.
class Pool(object):
"""A collection of P worker threads that distributes tasks
evenly across them.
"""
def __init__(self, size):
self.size = size
# create new workers based on size
self.workers = [Worker() for p in range(size)]
def do(self, tasks):
for p in range(self.size):
self.workers[p].inputs += tasks[p::self.size] # evenly distribute tasks
while any([len(worker.inputs) != 0 for worker in self.workers]):
pass # wait for all workers to finish
results = []
for worker in self.workers: # get results back from workers
results += worker.results
worker.results.clear()
return results # return complete list of results for all inputs
def __del__(self): # stop workers when pool is shut down
for worker in self.workers:
worker.running = Falsedef timestep(x0, v0, G, m, dt, pool):
"""Computes the next position and velocity for all masses given
initial conditions and a time step size.
"""
N = len(x0)
tasks = [(i, x0, v0, G, m, dt) for i in range(N)] # create task for each body
results = pool.do(tasks) # run tasks
x1 = np.empty(x0.shape, dtype=float)
v1 = np.empty(v0.shape, dtype=float)
for i, x_i1, v_i1 in results: # rearrange results (probably not in order)
x1[i] = x_i1
v1[i] = v_i1
return x1, v1
def simulate(P, N, D, S, G, dt):
x0, v0, m = initial_cond(N, D)
pool = Pool(P)
for s in range(S):
x1, v1 = timestep(x0, v0, G, m, dt, pool)
x0, v0 = x1, v1How does simulation perform as function of \(P\)?
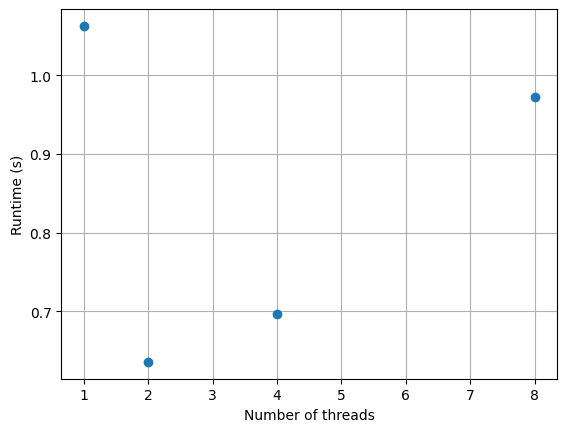
Multiprocessing
More like threading available in other languages…
Can’t be used directly from interactive interpreter; main module must be importable by fork processes
Provides Pool class for us, used with powerful map() function.
import numpy as np
from multiprocessing import Pool
def remove_i(x, i):
"""Drops the ith element of an array."""
shape = (x.shape[0]-1,) + x.shape[1:]
y = np.empty(shape, dtype=float)
y[:i] = x[:i]
y[i:] = x[i+1:]
return y
def a(i, x, G, m):
"""The acceleration of the ith mass."""
x_i = x[i]
x_j = remove_i(x, i) # don't compute on itself
m_j = remove_i(m, i)
diff = x_j - x_i
mag3 = np.sum(diff**2, axis=1)**1.5
# compute acceleration on ith mass
result = G * np.sum(diff * (m_j / mag3)[:,np.newaxis], axis=0)
return result
# function needs one argument
def timestep_i(args):
"""Worker function that computes the next position and velocity for the ith mass."""
i, x0, v0, G, m, dt = args # unpack arguments to original function
a_i0 = a(i, x0, G, m) # body of original timestep()
v_i1 = a_i0 * dt + v0[i]
x_i1 = a_i0 * dt**2 + v0[i] * dt + x0[i]
return i, x_i1, v_i1
def timestep(x0, v0, G, m, dt, pool):
"""Computes the next position and velocity for all masses given
initial conditions and a time step size.
"""
N = len(x0)
tasks = [(i, x0, v0, G, m, dt) for i in range(N)]
results = pool.map(timestep_i, tasks) # replace old do() with Pool.map()
x1 = np.empty(x0.shape, dtype=float)
v1 = np.empty(v0.shape, dtype=float)
for i, x_i1, v_i1 in results:
x1[i] = x_i1
v1[i] = v_i1
return x1, v1
def initial_cond(N, D):
"""Generates initial conditions for N unity masses at rest
starting at random positions in D-dimensional space.
"""
x0 = np.random.rand(N, D) # use random initial locations
v0 = np.zeros((N, D), dtype=float)
m = np.ones(N, dtype=float)
return x0, v0, m
def simulate(P, N, D, S, G, dt):
x0, v0, m = initial_cond(N, D)
pool = Pool(P)
for s in range(S):
x1, v1 = timestep(x0, v0, G, m, dt, pool)
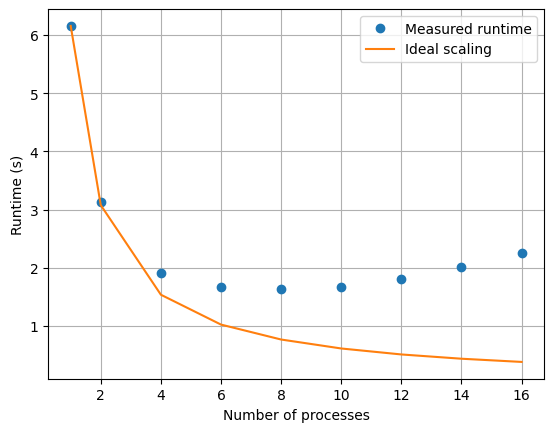
x0, v0 = x1, v1How does multiprocessing scale?
How does multiprocessing scale?
Other options for parallelism
MPI: Message-Passing Interface
Supercomputing is built on MPI.
MPI scales from hundreds of thousands to millions of processors.
Processes are called ranks and given integer identifiers; rank 0 is usually the “main” that controls other ranks. All about communication.
Can be used in Python and NumPy arrays with mpi4py
Numba
Numba is a just-in-time compiler for Python/NumPy
It translates Python functions to optimized machine code at runtime using the LLVM compiler—but does not require a separate compiler, just decorators
can automatically parallelize loops
Takeaways
If your problem calls for it, consider parallelizing.
That said, do not jump here, when implementing smart NumPy array operations, appropriate data structures, or existing solutions may suffice.